浅色/深色
算法入门
虞嘉乐21 计算机 4 班
提示
算法与计算机科学之间的密切关系
算法一词来自波斯的一名智者 —— 阿尔·花拉子密，他是 1000 多年前的代数之父之一。而计算机科学就是专门研究计算领域的现代学科。
排排坐，吃果果
记载最多的算法之一就是排序。要排序的内容多种多样，像给名字、数字又或者是其他什么东西按照某种规律排序，只有你想不到，没有不能排的。
可能你会觉得排序十分的简单呐，那么关于排序的算法又有多少呢？答案是超级多（当然，常用的只有十种）。
简单的尝试排序
咱们来试试简单的排序，在试排序之前，要讲一个东西：数组。数组如其名，就是一组数据组合起来的。为了更方便理解和解释排序算法，接下来会用一串具体的数字，见下图。（在这次排序中，我们使用的是从小到大的排列顺序。）
先找最小数，从最上面的 307 开始。在这个时候，307 就是最小的数字，因为现在只看到了这一个数字；然后是 239，比 307 小，所以新的最小数变成了 239；之后是 214，成为了新的最小数。在扫完所有数之后没有比 214 更小的数了，所以 214 移至最上方。接下来，从掉到第 2 位的 307 开始，继续重复之前的步骤，直至找到最小数 223，将 223 移至第 2 位。然后再继续重复步骤，一直到所有数都排列完毕，如下图
这种算法叫做选择排序，是常用的几种排序算法之一。用这种算法写的函数可以排序 8 个、8000 个或者 8 千万个数字都行。以下是排序选择的伪代码
简单看看这串代码，可以看见有两个 for 循环，这就意味着如果要排序 N 个东西，总共就要循环 N 的 2 次方次。
算法的复杂度
算法的输入大小和运行步骤之间的关系叫算法的复杂度，表示运行速度的量级。计算机科学家门把算法复杂度叫大 O 表示法（大写的 o）。算法复杂度
效率不高，前面的例子有 8 个元素，总共进行了 64 次循环，运行时间就是 64。如果把 8 个变成 800 个，那运行时间就是 640000。虽然大小只增长了 100 倍，但运行时间增加了 10000 倍！
随着数组增大，对效率的影响会越来越大，而大公司往往有几十亿条信息排序，所以必须要用更加高效的排序算法。
还是用之前的那个数组，也同样是从小到大排序，但使用另一个算法“归并排序”。第一件事是检查数组大小是否大于 1，如果是，就把数组分成两半，一直分成每个大小是 1 的数组。前置条件搞定了，现在可以归并了。从前两个数组开始，读数组内第一个值，这两个数组的值分别是 307 和 239，239 更小，所以放在旁边的第一位，307 放在第二位。重复这个过程后，按序排列，然后再归并一次。同样，取两个数组，比较第一个数是 239 和 214，所以 214 放在旁边的第一位；之后再次比较两个数组的第一位数 239 和 250，239 更小，放在旁边第二位；最后，再一次比较两个数组的数，250 和 307，250 更小，放在第 3 位，307 放在第四位，就这样，合成了一个更大的有序数组。然后再次重复这个步骤，得到另一个有序数组，最后这两个数组也分别用第一个值比较，这样就排好啦。
总之，归并排序的算法复杂度是 O(N*logN)。N 是需要比较 + 合并的次数，和数组大小成正比；logN 是合并步骤次数。这种算法的好处是，数组扩大了 1000 倍，分割次数也不会增大多少（log2 8000 约等于 13），但排序的元素多得多，因此合并算法效率更高。
蛮力什么的不要啦
为了引导下文，我们来谈一个经典的算法问题：图搜素。
图是用线连起来的一堆节点，一个节点到另一个节点的过程可以用成本或权重代称。如果无法理解，可以把它想成地图，节点是城市，线是路，每条路的长短不同，走这条路所花的时间就是成本或权重，可见下图
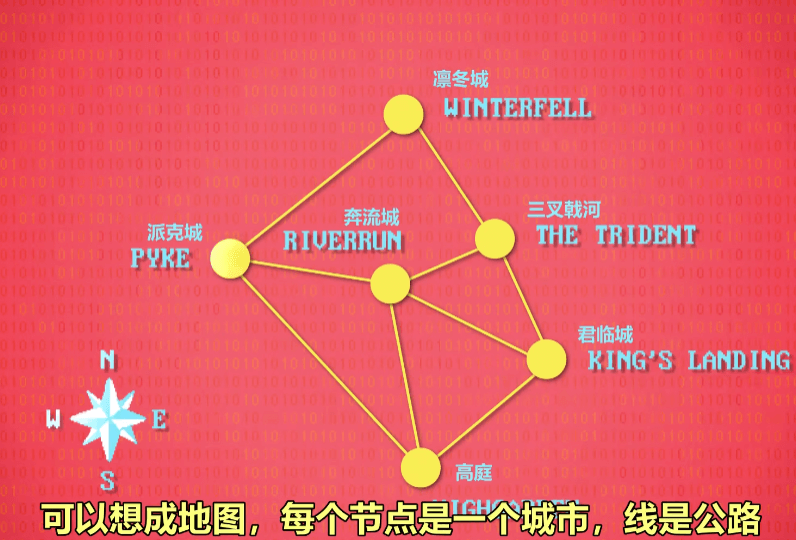
如果想要找到高庭到凛冬城的最短路径，最简单的方法是将所有的方式都尝试一遍，最后找到最短的一条。
用这种蛮力方法排列数组的时间复杂度是 O(n!)，n 是节点数，n! 是 n*(n-1)*(n-2)…… 一直到 1。这种方法比选择排序还要低效，所以，我们要用别的方法。
图搜索问题的经典算法的发明者是 Edsger Dijkstra，所以叫“Dijkstra 算法”。这种算法的复杂度和排序选择一样，是 O(n^2)，具体方式是：从起点出发（起点的成本是 0），记录周围所有节点最低的成本（用起点的成本加上到这个节点的成本），例子当中是君临城。然后先从君临城出发，同样记录周围节点最低的成本，然后用第 2 的奔流城，由于奔流城到三叉戟河的成本低于君临城到三叉戟河的成本，所以三叉戟河原本记录的成本被覆盖掉。最后，两条直接到达凛冬城的节点中选择成本最小的出发，并记录下来成本，与另一条路进行比较，选出成本小的一条路。下图更方便理解
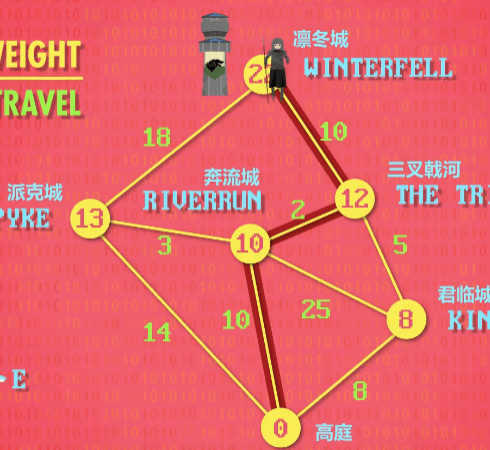
Dijkstra 算法的原始版本后死于 1956 年，这导致他的效率不够好，不能输入更多的数据。但后来得到了改善，变成了 O(N*logN+L)，N 是节点数，L 是多少条线。虽然看起来复杂了，但实际上快了很多。同样用之前的例子，原本的方法确定最小成本要 36 次，但新版只要 14 次左右。
总结
不论是排序也好，图搜索算法也好，都有着各自不同的优缺点，我们应该根据具体情况来使用或自己编写算法。
下一章
数据结构